| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Today
- Total
- activation function
- AdaGrad
- adaptive learning rate
- arithmetic reasoning
- Attention is all you need
- attention mechanism
- auto encoder
- Back Propagation Trough Time
- Backpropagation
- Bayes Theorem
- BCE
- Bert
- Bidirectional Encoder Representation from Transformer
- Binary classification
- BPTT
- Chain-of-Thought
- CNN
- commonsense reasoning
- Computer Vision
- Confusion Matrix
- convolutional neural network
- Cot
- cot reasoning
- counting
- Cross Entropy Loss
- deep learning
- degradation
- Dimension Reduction
- Few-shot
- fine-tuning
데이터 분석 일지
[Deep Learning] Linear Regression (선형 회귀) 본문
[Deep Learning] Linear Regression (선형 회귀)
-ˋˏ ♡ ˎˊ- 2024. 1. 23. 16:080. Purpose
선형 데이터에서 올바른 예측을 하기 위하여 Loss 값을 최소화시키는 방향으로 파라미터를 업데이트해야 한다. Gradient Descent를 사용하여 최적의 선형 그래프를 찾는 것이 목표이다.
1. Parameter Optimization using Gradient Descent
총 데이터 수는 N개이며 입력 데이터는 n차원이고 출력 데이터가 m차원일 때, 각 입력 데이터마다 출력 데이터가 있으므로 각 데이터 쌍은 아래의 수식과 같이 표현할 수 있다.
$$D = {(x_i, y_i)}{^N_{i = 1}}$$
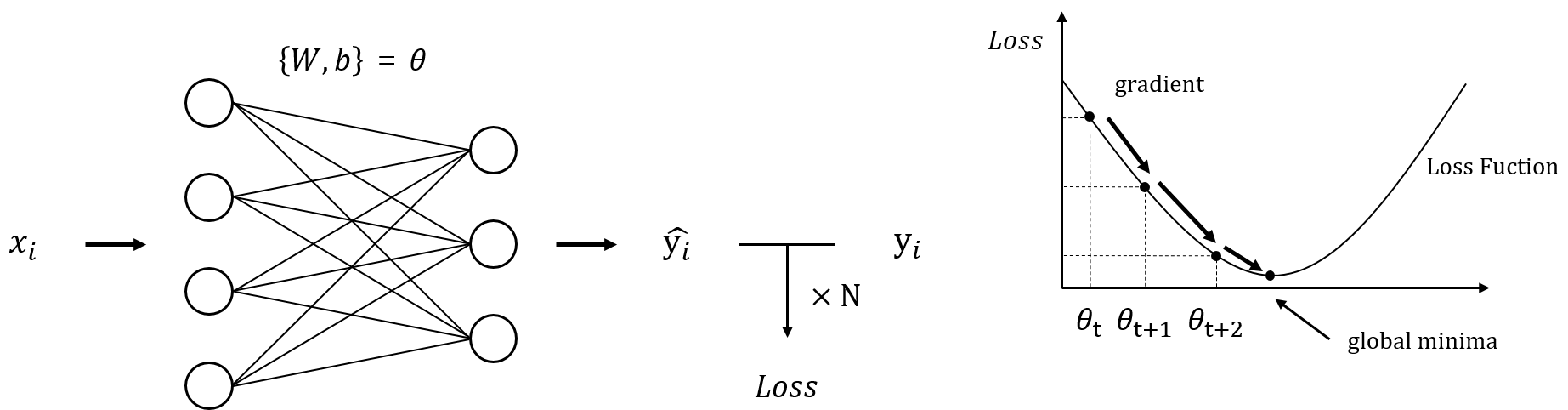
선형회귀는 위의 그림과 같이 입력 데이터가 선형 레이어를 지나 예측 데이터 y_i_hat을 도출해 내면 실제 출력 데이터 y_i와의 Loss 값을 구하고, Loss를 최소화하기 위해 Gradient Descent를 통한 파라미터 업데이트 과정을 거친다. Gradient Descent를 반복하여 Loss를 최소화하다 보면 목표 지점인 global minima에 다다르게 된다.
2. Loss Minimization using Gradient Descent - Detail
Gradient Descent를 활용하여 Loss를 최소화하는 방법을 자세히 설명하자면, Loss Function을 θ로 미분하여 기울기 값을 구하면 된다.
$$ \theta \leftarrow \theta - \eta \nabla _ \theta L( \theta )$$
기울기가 음수면 양의 방향, 양수면 음의 방향으로 나아갈 수 있다. 이는 점차 y 값이 작아지는 쪽으로 나아가게 된다.
'Lecture or Textbook Review > Deep Learning' 카테고리의 다른 글
| [Deep Learning] Regression (0) | 2024.01.31 |
|---|---|
| [Deep Learning] Logistic Regression (로지스틱 회귀) (0) | 2024.01.23 |
| [Deep Learning] 기초 최적화 방법: Gradient Descent (0) | 2024.01.22 |
| [Deep Learning] 신경망 학습 성능 판단 (0) | 2024.01.22 |
| [Deep Learning] 딥러닝 개요 (0) | 2024.01.22 |



